Rを用いて主観的等価点(PSE)を求める
目次
はじめに
恒常法を用いた実験などでは、得られたデータに非線形の関数をあてはめる(フィッティングする)必要があります。ここでは、フリーの統計ソフトRを 用いて、累積正規分布関数をあてはめて主観的等価点(PSE)を求める方法(プロビット解析)について簡単に説明します。(詳しい使い方は、末尾の参考文献などを参考にして、ご自身でご確認ください)
※ これ以降、この文の背景色で表した部分はRでのコマンド操作を表すこととします。
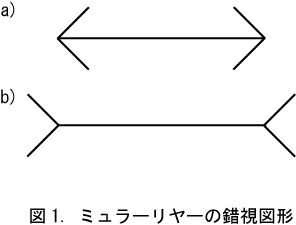
ここでは、ミュラーリヤー錯視の錯視量を測定する実験を例にあげて説明します。
ミュラーリヤー錯視図形(図1)では、水平線分の長さが同じであるにも関わらず、外向きと内向きの矢羽がつくことによって、水平線分の長さが異なって見えます。
ミュラーリヤーの錯視量がどれぐらいなのかを測定するために、次のような実験を行いました。
実験刺激は、図1a(図1上)と図1b(図1下)で、水平線分の長さが異なる a の形状の矢羽根を11個準備しました( b の水平線分の長さを基準として、-2.5°, -2.0°, -1.5°, -1.0°, -0.5°, 0°, 0.5°, 1.0°, 1.5°, 2.0°, 2.5°の11水準)。a の線分の長さがマイナスの場合は a の水平線分が b の水平線分に比べて短いことを、プラスの場合は a の水平線分が b の水平線分に比べて長いことを示しています。
実験参加者は、b の図形と比べて a の図形の水平線分が長いと思ったら1を、短いと思ったら0を回答しました。
独立変数を x、従属変数を y とします。yは観察者の回答になりますが、0か1かの2値のデータである必要があります。0と1のデータでない場合は、エクセルなどでデータを変換しておいてください。
この実験では、独立変数(x)が11水準で、各水準を20回繰り返しています。つまり得られたデータの数は220です。
サンプルデータとしてエクセルファイルとテキストファイル(CSV)を準備しました。いずれかをダウンロードしてください。
独立変数と従属変数をRに入力する
エクセルファイルを使用する場合
まずx,yの部分も含めて全てのデータをコピーします。
コピーしたデータはクリップボードというところに保存されているので、そこから読み込みます。
dat <- read.delim("clipboard")
※ Macではうまく動作しない場合があるようです。そのときは、CSVから読み込む方法を試してください。
テキストファイル(CSV)を使用する場合
「ファイル」→「ディレクトリの変更」(Macでは「その他」→「作業ディレクトリの変更」)を選択し、テキストファイルを保存しているディレクトリ(フォルダ)を選択する。
dat <- read.csv("sampledata.csv")
以上の操作の後、コマンドラインにdatと打ち込むと、正しく(x, y)が入力されているかを確認することができます。
最尤法を用いたプロビット解析
プロビット解析によって、累積正規分布関数の逆関数Φ-1(x)に線形モデル
Φ-1(x)=a+bx・・・(1)
を仮定して、aとbを求めます。xは独立変数です。
※ Φの後の-1は、マイナス1(引き算)を意味するのではなく、逆関数を意味しています。Φの右上に-1を記します。
Rでは次のコマンドを実行することで、aとbを求めることができます。
attach(dat) #datは前述のデータフレーム
m1 <- glm(formula = y ~ x, family = binomial(probit))
※ ブラウザによってはチルダが正しく表示されないことがあるようです。yとxの間の記号はチルダです。
次のコマンドを実行するとプロビット解析の結果が表示されます。
summary(m1)
m1から係数(a, b)を取り出し変数c1に代入します。
c1 <- coefficients(m1)
コマンドラインにc1と打ち込むと次のように表示されます。
| (Intercept) | x |
|---|---|
| -0.3894085 | 0.8882046 |
左(c1[1])がaの値、右(c1[2])がbの値になります。
ここで、μを知りたい分布の平均値、σを知りたい分布の標準偏差とすると、式(2)で表される標準化の関係式(Z変換)が成り立ちます。
Φ-1(x)=(x-μ)/σ・・・(2)
式(1)と(2)より次の式を導くことができます。
μ=-a/b
σ=1/b
aとbはすでに求まっていますから、μとσを計算することができます。
変数p1にμとσを代入します。
p1 <- c(-c1[1]/c1[2],1/c1[2])
コマンドラインにp1と打ち込んで次のような結果が表示されれば成功です。
| (Intercept) | x |
|---|---|
| 0.4384221 | 1.1258668 |
左の値は平均値(μ)で、回答の比率が50%となるときの刺激量、つまり閾値を表します。右の値は標準偏差(σ)です。
また回答の比率が75%となるときの刺激量を求めたい場合には、次の計算を行います。
qnorm(0.75, p1[1], p1[2])
グラフの作成
プロビット解析の結果をグラフで表すためにRでグラフを作成します。
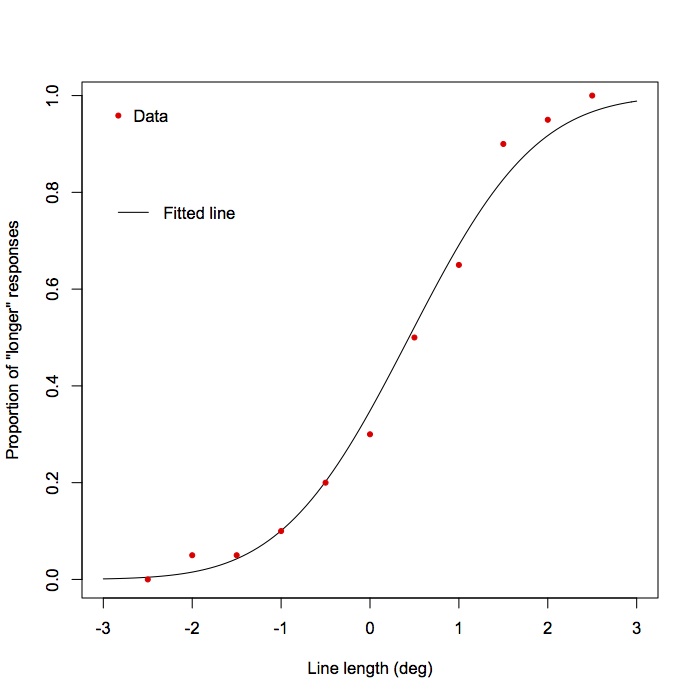
myfunc <- function(x) pnorm(x, p1[1], p1[2])
plot(myfunc, -3, 3, xlab="Line length (deg)", ylab="Proportion of \"longer\" responses")
これで累積正規分布関数がプロットされますが、実際に実験で得られたデータをプロットしてみないことには、どれぐらいあてはまっているか視覚的に分かりません。ここでは、エクセルなどで各水準ごとに回答の比率を出して、それをプロットする方法を示します。
各水準ごとに回答の比率をリスト化したテキスト(CSV)ファイルを準備します(前述したようにクリップボードを経由する方法でもかまいません)。テキスト(CSV)ファイルをダウンロードしてください。
dat2 <- read.csv("proportion.csv")
points(dat2, pch=20, col="red")
凡例を表示するには次のようにします。
legend(-3, 1, "Data", pch=20, col="red", box.lty=0)
legend(-3, 0.8, "Fitted line", lty=1, box.lty=0)
グラフをリセットしたいときは次のコマンドを実行してください。
frame()
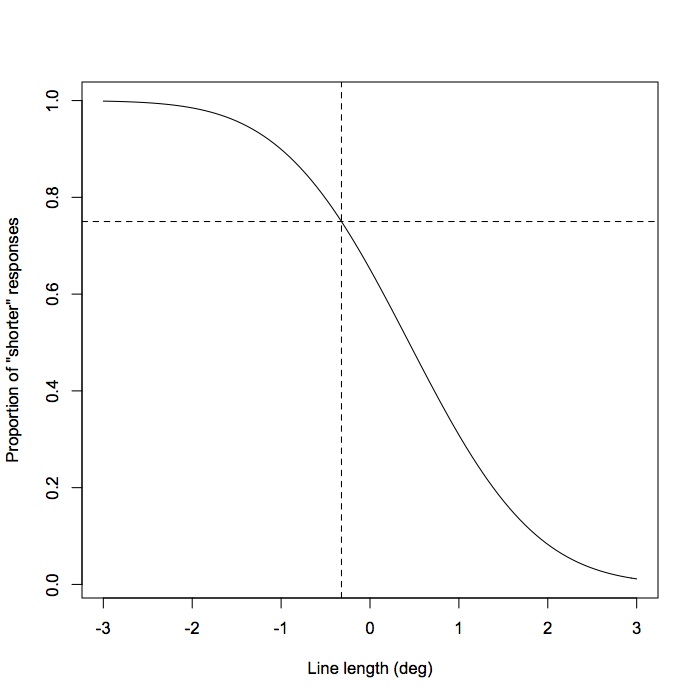
図1aの線分が”短い”と答えた割合をグラフに表したい場合
pnormの計算結果が、図1aの線分が”長い”と答えた割合なので、1からpnormの値を引くことで、”短い”と答えた割合を計算することができます。
myfunc2 <- function(x) 1-pnorm(x, p1[1], p1[2])
plot(myfunc2, -3, 3, xlab="Line length (deg)", ylab="Proportion of \"shorter\" responses")
もしローデータにおいて、”短い”と回答した場合を1、”長い”と回答した場合を0と割り当てている場合には、1と0を反転させて、プロビット解析を行う必要があるので注意してください。
また回答の比率が75%となるときの刺激量(線分の長さ)を求めたい場合には、次の計算を行います。
length <- qnorm(1-0.75, p1[1], p1[2])
グラフに破線をつけて、得られた閾値を確認してみましょう。
abline(h=0.75, lty=2)
abline(v=length, lty=2)
グラフをR以外のアプリケーションで利用するには
Windowsではグラフを右クリックして、「メタファイル」または「ポストスクリプト」に保存することが可能です。画像として保存せずに、コピーをして他のアプリケーションに貼り付けることも可能です。
Macではグラフを選択した状態で、「ファイル」→「別名で保存」を選択するとPDFファイルとして保存することが可能です。
参考リンク・文献
- R-Tips
- Rで統計
- Rによる統計処理
- RjpWiki
- 中村知靖・松井仁・前田忠彦. 心理統計法への招待. 統計をやさしく学び身近にするために. サイエンス社
- 舟尾暢男. The R Tips. データ解析環境Rの基本技・グラフィックス活用集. 九天社
- Maindonald, J., & Braun, J. Cambridge Series in Statistical and Probabilistic Mathematics. Data Analysis and Graphics Using R. An Example-based Approach. CAMBRIDGE UNIVERSITY PRESS.